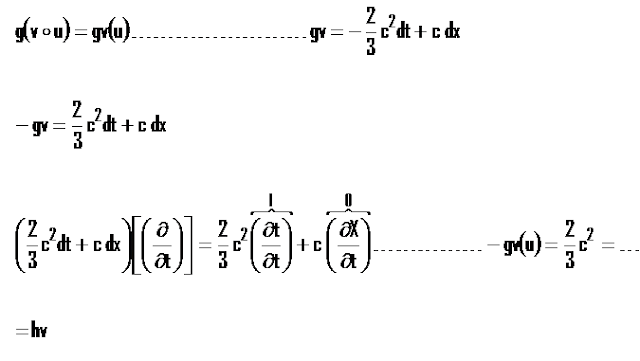
TAREA 14# A -BIVECTOR...
DEMUESTRE QUE
TAREA 14#B ´´TRIÁNGULO DE PASCAL´´
En el triángulo de pascal la primer columna de izquierda a derecha ( la de los 1) representa a los escalares, y tiene valor absoluto 1 debido a que cualquier número real multiplicado por uno asigna una magnitud, el escalar es que el que cumple el objetivo de la asignación del valor de la magnitud del vector, bivector, trivector....Etc.
La segunda columna (1,2,3,4...Etc, es la de los vectores, y nos dan la idea de que dimensión estamos tratando).Hay que recordar que un vector es la tangente a una curva, por ello si estamos en el caso de un ´´universo´´ dimensión 1 sólo tendremos un vector. En cambio aumentaran si también incrementamos la dimensión de nuestro ´´universo´´.
Los bivectores los encontramos en la siguiente columna (1,3,6....) estas son las tangentes a superficies, por consiguiente, como son tangentes se les representa también como las derivadas parciales, como son para una superficie, por cada dos superficie que ´´entre´´ en las dimensiones de nuestro ´´universo´´ habrá entonces un bivector.
La última columna (1,4...) es la tangente a un volumen, por eso si tenemos un universo dimensión 3 ( sólo voumen) tendremos un sólo trivector....
La segunda columna (1,2,3,4...Etc, es la de los vectores, y nos dan la idea de que dimensión estamos tratando).Hay que recordar que un vector es la tangente a una curva, por ello si estamos en el caso de un ´´universo´´ dimensión 1 sólo tendremos un vector. En cambio aumentaran si también incrementamos la dimensión de nuestro ´´universo´´.
Los bivectores los encontramos en la siguiente columna (1,3,6....) estas son las tangentes a superficies, por consiguiente, como son tangentes se les representa también como las derivadas parciales, como son para una superficie, por cada dos superficie que ´´entre´´ en las dimensiones de nuestro ´´universo´´ habrá entonces un bivector.
La última columna (1,4...) es la tangente a un volumen, por eso si tenemos un universo dimensión 3 ( sólo voumen) tendremos un sólo trivector....
TAREA 14#C ´´MNR Y EL TRIÁNGULO DE PASCAL´´
Un núcleo puede estar acoplado a más núcleos y el desdoblamiento (si todas las constantes son iguales) viene dado por el triángulo de Pascal:
Núcleos acoplados
|
Intensidades
|
Desdoblamiento
| ||||||||||||||
0
|
1
|
Singlete (s)
| ||||||||||||||
1
|
1
|
1
|
Doblete (d)
| |||||||||||||
2
|
1
|
2
|
1
|
Triplete (t)
| ||||||||||||
3
|
1
|
3
|
3
|
1
|
Cuadruplete (q)
| |||||||||||
4
|
1
|
4
|
6
|
4
|
1
|
Quintuplete (quint)
| ||||||||||
5
|
1
|
5
|
10
|
10
|
5
|
1
|
Sextuplete
| |||||||||
6
|
1
|
6
|
15
|
20
|
15
|
6
|
1
|
Heptuplete
| ||||||||
Lo cual se interpreta como
En una MRN los resultados obtenidos con respecto al número de átomos de hidrógeno acoplados puede ser equiparable a la dimensión que viene dada en el triángulo de Pascal, así cuando no hay un H que este unido al C para acoplaser con otros átomos de H que estén como sustituyentes para el C la dimensión 0 del triangulo de pascal nos dice que no hay algun H enlzado a ese C. Así pues las dimensiones del triángulo de Pascal nos representan el número de H que esten enlazados a un carbono de la cadena alifática ó anillo principal ( que tenga enlace C-C)
Como se sabe, los 1 del lado izquierdo son sólo un escalar, es para asignar la magnitud, los términos que se encuentre después de ese 1 nos representan los espectros absorbidos por dichos núcleos, y el número que tengan es la intensidad con la que se emite cada ´´linea´´ el espectro .
Como se sabe, los 1 del lado izquierdo son sólo un escalar, es para asignar la magnitud, los términos que se encuentre después de ese 1 nos representan los espectros absorbidos por dichos núcleos, y el número que tengan es la intensidad con la que se emite cada ´´linea´´ el espectro .
El triángulo de Pascal es una ayuda que
permite conocer, en primera aproximación las intensidades esperadas de las
diferentes absorciones en un espectro de resonancia magnética nuclear.
INTENSIDADES
Nº de vecinos
1 0
1 1
1
1 2 1 2
1 3
3 1 3
1 :
4 6 4
1
4
1 5
,10 10
5 1 5
1 6
15 20 15
6 1 6
:1 7
21 35 35
21 7 1 7
etc...
etc..
------------------------------------------------------------------------------------------------------------
El Triángulo
de Pascal es útil para asignar teóricamente la intensidad en las absorciones de
los multipletes en espectros simples.
TAREA 14#D
´´EVALUACIÓN DE LA DERIVADA DE GRASSMAN´´
TAREA 14#E
